Ebben a posztban megpróbálom öszefoglalni a méltán elhíresült "Padding Oracle Attack" lényegét, ami bizonyára nem kevés álmatlan éjszakát okozott néhány programozónak és egy rakás üzemeltetőnek. 

Matekozni fogunk, szóval igyatok egy kávét vagy ilyesmi!

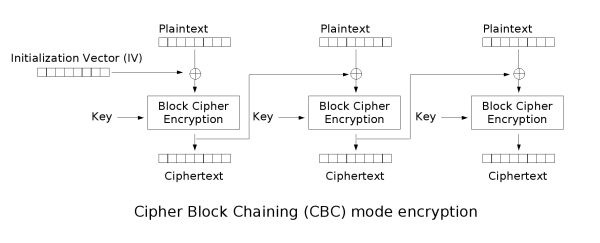
A legalapvetőbb tudnivaló, hogy a támadás CBC (chipher block chaining) módú blokktitkosítókkal szemben működik. Ennek a működési módnak a lényege, hogy a blokktitkosító eljárást mindig a nyílt szöveg és az előző blokk kriptoszövegének bitenkénti kizáró vagy összegére (a továbbiakban összeg, +) alkalmazzuk, így elkerüljük a sima ECB mód okozta problémákat, tűrhető hibaterjedés mellett. Az első nyílt szöveg blokkot egy szabadon választott inicializáló vektorral (blokk méretű bájtsorozat) adjuk össze, ezt nyílt csatornán továbbíthatjuk a kriptoszöveggel együtt.

A blokktitkosítókat általában úgy alkalmazzák, hogy a nyílt szöveget kiegészítik úgy, hogy annak mérete a blokkméret többszöröse legyen, ezt a kitöltést nevezzük paddingnek. Az egyik legelterjedtebb padding módszerre a PKCS #5 néven szokás hivatkozni, ennek lényege, hogy a kitöltés bájtjainak értéke megegyezik a kitöltés hosszával, valamint mindig sor kerül legalább egy kitöltő bájt hozzáfűzésére a nyílt szöveghez - blokkhatárig tartó bemenet esetén egy teljes blokknyi paddinget alkalmazunk. A támadás szempontjából ez utóbbi tulajdonság lesz lényeges, illetve fontos, hogy a padding legalább megjósolható legyen (véletlen értékek esetén nem rúgunk albdába)

Képletekkel az első blokkra tehát:

• C=E(P+IV)
• P=D(C)+IV

A támadás alapját (és nevét) továbbá az adja, hogy szökségünk van egy rendszerre, amely tetszőleges IV-kriptoblokk párra megmondja, hogy helyes-e a padding. .NET-es webalkalmazások esetében ez úgy nézett ki, hogy a szerver 500-as Internal Server Errort (PaddingException) dobott vissza hibás padding esetén, egyébként 200-at.

Vegyük a kriptoszöveg egy blokkját, és egy csupa NULL-byte-ból álló IV-t, a duót pedig küldjük el az orákulumnak. Az orákulum nagy eséllyel azt fogja mondani, hogy a padding rossz, ezért újrapróbálkozunk az IV utolsó bájtjának inkrementálásával. Az eljárást addig folytatjuk, amig az orákulum elégedett nem lesz. Legyen ekkor az IV utolsó bájtjának értéke X. Elég jó esélyünk van arra (bár valójában nem lehetünk biztosak benne...), hogy az orákulum belső dekriptáló eljárásan kimenete blokkméret-1 bájtnyi szemetet, valamint egy 1 értékű bájtot eredményezett mint nyílt szövegblokk (hiszen ez egy érvényes padding). Ekkor tudjuk, hogy

0x01=X+<D(C) utolsó byte-ja>  (*)

mindkét oldalhoz hozzáadva az eredeti IV utolsó byte-ját és X-et (blokkméretű tagok esetén a blokk utolsó bájtját értéstek oda):

• IV+X+0x01=X+D(C)+IV+X=
  =X+P+X=
  =P

Az egyenlőség bal oldalának minden tagja ismert, a jobb oldalnak meg örülünk :) Ugyanezt a módszert folytathatjuk visszafelé haladva az IV byte-jain, szépen sorban megkapva a nyílt szöveget. 

Ami ezt a támadást a .NET-es webalkalmazásokra nézve különösen veszélyessé teszi az az, hogy ugyanígy elvégezhető tetszőleges nyílt szöveg titkosítása is a Padding Oracle segítségével!

Ismét a (*) egyenletből kiindulva:

• X+0x01=X+<D(C) utolsó byte-ja>+X=<D(C) utolsó byte-ja>

vagyis D(C) megkapható, így

• Pi=D(Ci)+Ci-1

miatt az Ci-1 beállításával meghatározható Pi. Fontos megérteni, hogy ez az utolsó lépés az "orákulumban" történik: az általunk adott bemenet Ci és Ci-1 és azt szeretnénk, hogy Pi általunk választott legyen, anélkül, hogy ismernénk D() kulcsát. 

Vegyük észre, hogy az eljárás során "tönkre kell tennünk" (Ci-1)-et, ahhoz, hogy Ci-re jó Pi-t kapjunk. A (Ci-1)-re kapott Pi-1 kimenetet viszont helyreállíthatjuk Ci-2 megfelelő beállításával, és így tovább egészen az IV-ig, aminek a megváltozása jó esetben nem zavar senkit. Persze vannak alkalmazások, ahol az IV rögzített, ilyenkor a nyílt szöveg első blokkja használhatatlanná válik.

A DotNetNuke vesztét az okozza, hogy ezzel a módszerrel létrehozható olyan titkosított süti, ami megmondja a rendszernek, hogy mi bizony adminok vagyunk.

Ez lenne tehát a probléma lényege, igazából nem kell hozzá matematikusnak lenni, hogy az ember megértse. Ettől függetlenül előfordulhat, hogy az interpretációm nem kristálytiszta, kommentben kérdezzetek nyugodtan, vagy olvassátok el Juliano Rizzo és Thai Duong eredeti esszéjét.